Data Representation
What the Specification Says:
Demonstrate an understanding of floating point representation of a real binary number;Â
Normalise a real binary number;Â
Discuss the trade-off between accuracy and range when representing numbers.
Number Systems
Introduction
When we count we usually use the denary number system, which is base 10. We count from 0 to 9, and then put a 1 in front and start again. Computers find it easier to work with binary, which is base 2, because it is only 0s and 1s, which can represent on or off, yes or no, or true or false,
Converting from Denary to Binary
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
|
|
|
|
|
|
|
To turn a denary number into a binary number, just put 1s in each column which is needed to make the number, using the column headings below. We usually work with 8 bits at a time, which is about 1 byte, so if the number is smaller; we need to put in leading zeros.
For
example: 7510 in binary would be equal to 010010112 in binary,
because 75 is the same as no lots of 128, one lot of 64, no lots of 32 or 16, one lot
of 8, no lots of 4, and one lot of 2 and 1.
Converting from
Denary to Octal
Octal is base 8, the principle for converting
from denary to octal is similar as to that of denary to binary, although the column
headings are obviously different, and you can have up to 8 lots of a number in each
column.
|
512 |
64 |
8 |
1 |
|
|
|
|
|
For example 7510 in denary would be no lots of 512, one lot of 64, one lot of 8 and three lots of 1, so it would be 01138 in octal.
Â
|
Hex Letter |
Denary Representative |
|
A |
10 |
|
B |
11 |
|
C |
12 |
|
D |
13 |
|
E |
14 |
|
F |
15 |
Converting from
Denary to Hexadecimal
Some information is stored in computers as
numbers in base 16, or hexadecimal sometimes just called hex. The principles are
exactly the same for binary, octal, denary or any other base. But if you have to be
able to count from 0 to 15, we would have to have 16 digits, as we only have ten (0
to 9) we have to use letters after that.
|
256 |
16 |
1 |
|
|
|
|
For example; 7510 in denary will be four lots of 16 and eleven lots of 1, so it is equal to 4B16 in hex.
Â
Binary Coded
Decimal
Some numbers look like numbers, but
don’t behave like numbers, for example you can not add together barcodes. Binary Coded Decimal (BCD) just
represents four different digits in the number separately, using four binary digits
for each denary digit.
|
8 |
4 |
2 |
1 |
|
|
|
|
|
|
+/- |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
|
|
|
|
|
|
|
For example; 710 would be equal to 01112 because it is no lots of 8 and one lot of 4, 2 and 1. 510 would be equal to 01012. So 75 in BCD would be 01110101 (just put the two together).
Negative Binary -
sign magnitude
In sign magnitude method of storing negative
binary numbers, the first bit, where the 128 was becomes a +/- bit, if there is a 1
here it is negative, whereas a 0 indicates that it is a positive binary
number.
For example -7510 would
be = to 110010112.
There are two problems with this method, firstly the biggest number that can be stored in one byte is half what it was, and secondly it is now storing two different types of data, a sign and a value, this makes it harder to do arithmetic operations.
|
-128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
|
|
|
|
|
|
|
Â
Negative Binary -
Twos complement
This gets round the problems with the sign
magnitude method, in 2s complement the first bit of the bye becomes -128. 2s
complement is very useful for addition and subtraction, because the negative part
will do its self, and all we need to do is add it.
For
example: -7510 would start with a 1, because it is a minus, we then work
upwards adding more digits to get it up from -128 to -75. We need 53 to get up to -75
which is equal to 1 lot of 32, 16, 4 and 1. So -75 denary
is equal to 10110101 in 2s complement binary.
Addition of Binary
numbers
Addition in binary is much more simple than
addition in denary, so computers can do it much faster, there are only four possible
sums in binary:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, carry 1
For example 75 + 14 in
denary:
          Â
-128Â Â
64Â Â Â Â Â Â
32Â Â Â Â Â Â
16Â Â Â Â Â Â
8Â Â Â Â Â Â Â Â Â
4Â Â Â Â Â Â Â Â Â
2Â Â Â Â Â Â Â Â Â
1
75 =Â Â Â 0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1
14 = Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0
          Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
= 89
Carry                                    Â
1Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â
1
Subtraction of Binary
numbers
We
use 2s complement when doing subtraction of binary numbers,
(because 75 – 14 is the same as 75 + (-14)). When we do
subtraction of binary nun umbers, we never do any subtraction;
it’s all addition
For example, 75 –
14
-128Â Â 64Â Â Â Â Â Â
32Â Â Â Â Â Â
16Â Â Â Â Â Â
8Â Â Â Â Â Â Â Â Â
4Â Â Â Â Â Â Â Â Â
2Â Â Â Â Â Â Â Â Â
1
75 =Â Â Â 0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1
14 = Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0
          Â
0Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
0Â Â Â Â Â Â Â Â Â
1Â Â Â Â Â Â Â Â Â
= 61
Carry 1                                 Â
                                              Â
1
Floating Point Binary
This text presumes we already know how to convert to and from binary numbers, and can represent both negative and positive.
Floating point binary is used to represent fractions.
The model for a whole number byte: 128 64Â Â Â Â Â Â Â 32Â Â Â Â Â Â Â 16Â Â Â Â Â Â Â 8Â Â Â Â Â Â Â Â Â 4Â Â Â Â Â Â Â Â Â 2Â Â Â Â Â Â Â Â Â 1
Where each sub heading will have either a one or a zero under it depending on what the value of the number.
Effectively there is a decimal point at the end of this number. (e.g. 139 = 139. = 139.0)
Also each heading it the heading before divided by two.
If we had a two byte representation of a binary number, with the second byte being the decimal point it would look like:
128Â Â Â Â 64Â Â Â Â Â Â Â 32Â Â Â Â Â Â Â 16Â Â Â Â Â Â Â 8Â Â Â Â Â Â Â Â Â 4Â Â Â Â Â Â Â Â Â 2Â Â Â Â Â Â Â Â Â 1Â Â Â Â Â Â Â Â Â ||Â Â Â Â Â Â Â Â Â 0.5Â Â Â Â Â Â 0.25Â Â Â Â 0.125 Ã
And so on. (the arrow is because there wasn’t room on the page to carry on, and it’s kind of obvious what’s going to come next).
However a major restriction of this is that the decimal point can’t be moved.
So instead we put the decimal point at the beginning of the binary byte and add put the point to the power of something. Like in base 10, we represent big numbers by doing for example 1.64 x 10 9 = 1,640,000,000 and  3.29 x 10 -4 = 0.000329 .
In binary we can have for the value of 2.75, 10.11 = .1011 x 210 = .001011 x 2100.
The point is moving.
The computer cannot cope with the point being in a different place from number to the next, because it has no way of representing the point.
As a result the decimal point is usually put before the first 1. There are however other options, but everyone’s got to use the same, in order for all computers to understand it.
So 2.75 which is equal to 10.11 would be represented as .1011 x 210. The x2 just shows how many decimal places it should be moved by in order to give the original number.
When the value is written like this, it is normalised, which means expressed in the same form as all the others.
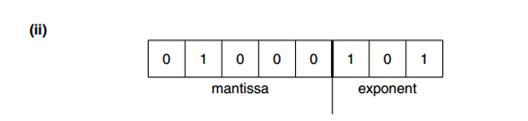
With the number, 0.1011 x 210, there are two parts. The 0.1011 is called the mantissa. The second part, after the x2 is 10 and is called the exponent.
So..                 Mantissa        ||         Exponent
                       01011            ||         010
Trade of between Accuracy and Range
If you increase the number of bits for the exponent (and subsequently decrease the number available for the mantissa), then the accuracy is decreased and the range (size of numbers that can be stored) is increased. This is important to remember.
Key Words
§ Mantissa – The part of the representation that contains the actual values. i.e. the first part.
§ Exponent – The part of the representation that shows how many places the decimal point has to be shifted in order to return the original number.
§ Normalised – When the number is written in standard form.
Example
A number is represented as an 8 bit floating point number. 5 bits are used as the mantissa and 3 bits are used as the exponent. Both the mantissa and the exponent are in twos complement.
The floating point number is 01100010
a) Show the floating point in its denary equivalent
b) What is the number in decimal?
Step 1.Break the floating point number into its two parts and place a decimal point in the mantissa between the most significant bit and the next one:
Mantissa is 0.1100 because the question states it uses the first 5 bits.
Exponent is 010
Both are positive binary numbers because they have a leading zero. So the mantissa in denary form is 1100 -> 12 denary
The exponent is 010 -> 2 denary
Step 2.Slide the decimal point of the mantissa by the exponent value i.e. 2 places to the right
The floating point numbers represents 11.00 binary
or +3.0 decimal
Past Paper Questions and Answers
 |

                                                   Â

Question number four of all exam papers will involve a floating-point binary calculation